Introduction

This section is a continuation of the previous tutorial (see Singular Value Decomposition). Here we do not discuss any implementation issues (see Implementation).  

The basic equation is the integral equation of the first kind:

     (1)

The integral operator 

     (2)

connects two in general different spaces: the space of reconstructing functions f(x) and the space of measuring functions g(x). 

 

Definitions

Let  us define:

• U is a set of all functions (vectors) { u _n} (the complete basis set). 
• U₁ is a set of functions u _n corresponding to non-zero
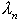
• U₂ is the rest of basis functions u _n
• V is the complete set of functions { v_n }
• V₁ = K U₁ (is a set of functions v_n corresponding to non-zero )
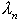• V₂ is the rest of basis functions v_n
• F is the space spanned by the set of vectors U. In other words, any vector f in U is a linear combination of all basis functions:
        f  = r₁ u₁ + r₂ u₂ + r₃ u₃ +  . . .
• The set of vectors U₁ spans a subspace F₁ of the space F
• The set U₂ spans the subspace F₂ 
• The basis set V forms the space of measuring functions G :  f  = s₁ v₁ + s₂ v₂ + s₃ v₃ +  . . 
• The subspace G₁ is spanned by the set V₁ 
• The subspace G₂ is spanned by the set V₂ 

 

3D-space Example

 The three-dimensional space has only three basis vectors: U = {u₁ , u₂ , u₃}. Let U₁ = {u₁ , u₂} then u₂ = { u₃}. The space F is the whole 3D-space. The subspace F₁ is the (u₁ , u₂)-plane (blue). The subspace F₂ is the u₃ -axis and not the rest of the space. 

In this example the space G is also formed by the set of three basis vectors V = {v₁ , v₂ , v₃}. The subspace G₁ is the (v₁ , v₂)-plane (green). The subspace F₂ consists of the u₃ -axis.

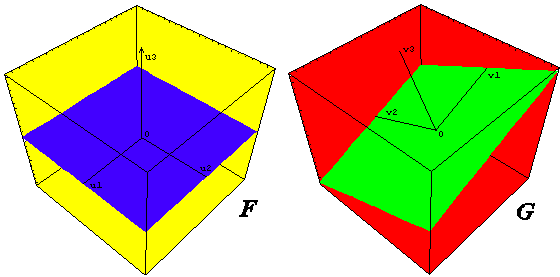F-space	G-space

Mapping of Spaces

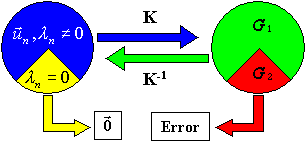
The operator (2) transforms the F-space in the following way

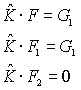
It maps the whole space F and the subspace F₁ to G₁. It maps the subspace F₂ to 0.

 

Interpretation of Mapping

The last of the above equations means that the F₂ components of a reconstructing function f do not produce the measuring signal in this experiment (instrument). This just reflects an incompleteness of this experiment. From the reconstruction viewpoint this is the source of instability of the inverse problem. 

The F₁ components produce a signal which is a function from the subspace G₁. This signal can be used for reconstruction of the unknown function. It can be done by means of pseudo-inverse operator. Although it is not necessarily the best practical method of reconstruction.

There are no components in the F-space that produce a signal in the G₂ subspace. If the right-hand side of the equation (1) contains components from the G₂ subspace, then the equation does not have a solution.

The following picture summarize the interpretation

 

 

Use of singular functions

The singular functions (vectors) are natural bases for the integral operator (1) or for a given method of measurement.

• The basis set U₁ is used for the construction of unknown function  f. Only this part of the reconstructing function can be determined from the experiment. However, the U₂ components can be used for additional shaping of the result, e.g. to make it smooth.
• The basis set V₁ should be used for a natural filtering of measuring functions. All the V₂ components of a signal must be filtered out before processing.

 

Experimental noise

In practice some random noise makes contribution to a signal:

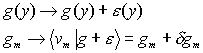
It causes errors in the coefficients of reconstructed function:

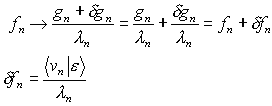
The noise amplification factor can be defined as 

 

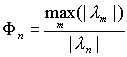
Reconstruction criterion 

Any f(x) that reproduces g(y) within an experimental errors is a solution of the equation (1). 

 

Units of Information

The above criterion further restricts the set of functions within G₁: only the components with the g_n above the noise level should be taken into account. It also limits the set of functions u_n which can be used for reconstruction. The number of singular functions involved in reconstruction is the actual number of the units of information available for this instrument and noise level.

 

Accuracy and Resolution

The number of functions and their shape gives the answer for the following important questions

• What is the accuracy of reconstruction?
• What is the resolution?
• What is the region where the unknown function can be reliably reconstructed?

The accuracy is the largest amplitude of the rejected functions. The resolution is the shortest half-wavelength of the functions that can be used for reconstruction.  

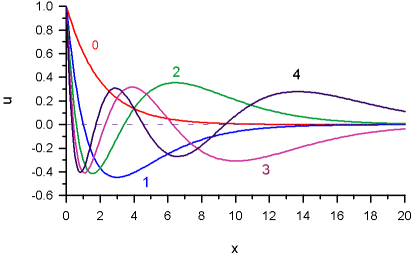Typical singular function behavior

Reliable Reconstruction Region

Extremely useful characteristics which is usually ignored, is Reliable Reconstruction Region, RRR. It can be defined as a region where are situated the nodes (zeros) of the functions u_n used for reconstruction. In the above picture the RRR is approximately [0.5, 10]. 

 

Accuracy and Interval of Measurements

The accuracy of measurements and the interval of measurements affect the overall accuracy, resolution and Reliable Reconstruction Region. Analytical calculations and numerical experiments (see Implementation) show the following:

• The accuracy of measurements increases the number of singular function and primarily increases accuracy and resolution of reconstruction
• The extension of the interval of measurements modifies the integral operator (by increasing the interval [c,d], see Basics of Indirect Measurements) and increases the Reliable Reconstruction Region (e.g. the depth of detection, or interval of sizes).

References

1. V.S.Bashurova, K.P.Koutsenogii, A.Yu.Pusep, N.V.Shokhirev. Determination of atmospheric aerosol size distribution functions from screen diffusion battery data: Mathematical aspects. J.Aerosol Sci., v.22, p.373-388, 1991.>
2. A.Yu.Pusep, V.S.Bashurova, N.V.Shokhirev A.I.Burshtein. The development of the software for NMR-tomography of underground water. Tech. Report of the Institute of Chemical Kinetics and Combustion. Academy of Sciences of the USSR, Novosibirsk, 1991.
3. N.V.Shokhirev, L.A.Rapatskii, A.M.Raitsimring. Electron-ion pair distribution function reconstructed from radiation-chemical and photochemical experiments. Chem.Phys., v.105, p.117-126, 1986.
4. A.Yu.Pusep, N.V.Shokhirev. Determination of particle-size distribution functions in aerosols from measurements by diffusion batteries. Colloid J., v.48, p.108-113, 1986.
5. N.V.Shokhirev, V.V.Konovalov, A.Yu.Pusep, and A.M.Raitsimring. Recovering the e-aq distribution in Photoemission. Theor.Exper.Chem., v.20, p.316-321, 1984.
6. A.Yu.Pusep, N.V.Shokhirev. Application of a singular expansion for analyzing spectroscopic inverse problems. Opt.Spectrosc., v.57, p.482-486, 1984.