Definitions, Formulae

Nikolai Shokhirev

- Definitions
- Distributions
- Multivar correlations
- Principal component analysis

Definitions

n-th moment		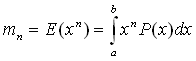(1)
Norm		(2)
Mean		(3)
n-th central moment		(4)
Variance		(5)
Std deviation		(6)
Skewness	μ₃/ σ³	(7)
Kurtosis	μ₄/ σ⁴	(8)
Excess kurtosis	μ₄/ σ⁴ - 3	(9)

Useful relations

μ₂= m₂ - m₁²	(10)
μ₃= m₃ - 3 m₂ m₁+ 2 m₁³	(11)
μ₄= m₄ - 4 m₃ m₁+ 6 m₂ m₁² - 3 m₁⁴	(12)

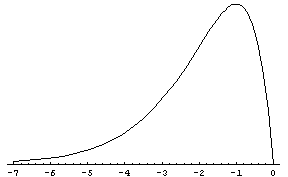
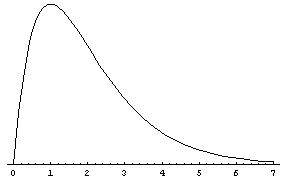
Skewness example

Power-exponential function:


Negative skew, left-skewed.	Positive skew, right-skewed.

See more examples in Distributions.

Kurtosis terminology

A high kurtosis distribution has a sharper "peak" and flatter "tails", while a low kurtosis distribution has a more rounded peak with wider "shoulders".

Distributions with zero excess kurtosis are called mesokurtic, or mesokurtotic. The most prominent example is the normal distribution.
A distribution with positive excess kurtosis is called leptokurtic, or leptokurtotic. Laplace distribution (double exponential distribution), excess kurtosis = 3.
A distribution with negative excess kurtosis is called platykurtic, or platykurtotic. Uniform distribution, excess kurtosis = -1.2.

Laplace distribution.

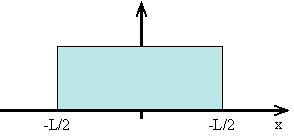
Uniform distribution.

See more examples in Distributions.

Sample estimators

In practice, often the density functions P(x) are not available and only a limited number of a random variable is available: x_i , i = 1, . . . , N . So-called sample estimators can be used instead of (1):

n-th moment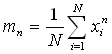

(13)

Note, that m_n as the sum of random variable is a random variable itself. It has its expectation (mean) value and standard deviation. An estimator is called "unbiased" if its expectation value is equal to the exact (population) value. For example, E(m₁) = μ, is an unbiased estimator; E(m₂ - m₁²) = σ² N/(N - 1), is biased (although it tends to σ²as N → ∞).

Unbiased estimators

Mean	m₁	(14)
Variance		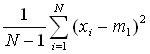(15)
Skewness		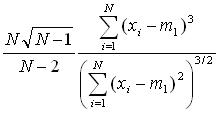(16)
Excess kurtosis		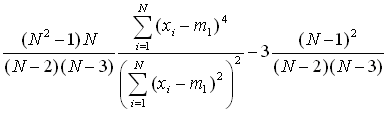(17)

References

- Definitions
- Distributions
- Multivar correlations
- Principal component analysis