Indirect and Remote measurements
Singular Value Decomposition
Nikolai Shokhirev
- Singular Value Decomposition
- Analysis of accuracy and resolution
- Implementation
Introduction
In many experiments the unknown functions f(x) is connected with the measured signal g(y) by an integral equation of the first kind:
![]() (1a)
(1a)
A broad class of such inverse problems is instrument distortions of spectra. Indirect measurements in which g(y) and f(x) are different physical dependences are also described by the above equation. For example, g(y) is the decay of the electron spin echo amplitude, while f(x) is the distribution function of radical pairs over distances. This equation can be also written in the operator form:
![]() (1b)
(1b)
The integral operator is a mathematical model of an experiment (instrument). The operator consists of three "parts":
-
The kernel K(y, x), which is the response of the instrument
to the pulse (
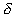 -function) input
:
-function) input
:
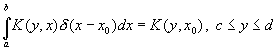
-
[c, d] is the interval of reconstruction (determination)
- [a, b] is the interval of measurement (scanning interval)
![]()
- Reconstruction of g(x) and
- Analysis of accuracy and resolution
Now we discuss the a very efficient method of the analysis of accuracy and resolution of the solution and the influence of experimental accuracy and the interval of measurements.
Notations We will use the notation suitable both continuous functions
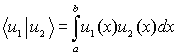
and vectors
![]()
The same notation will be used for the y-space (the interval [c, d] ). The two spaces are different, but it will be clear from a context which one is currently considered.
Singular Value Decomposition
The kernel allows the following expansion (in general infinite):
![]() (2)
(2)
In linear algebra such expansion is called Singular Value Decomposition (SVD).
Here ![]() are the singular values and vn and un are
the singular functions (vectors). Within each set the functions can be chosen
orthogonal and normalized:
are the singular values and vn and un are
the singular functions (vectors). Within each set the functions can be chosen
orthogonal and normalized:
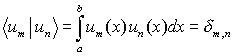 (3a)
(3a)
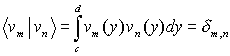 (3b)
(3b)
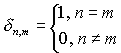
Completeness of singular basis sets
The two sets of basis functions (or vectors) {vn}and {un}are not necessarily complete (in each space). However we always can expand SVD with necessary additional functions and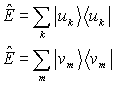 (4)
(4)
![]()
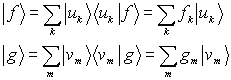
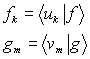
are the expansion coefficients.
Formal solution
The integral equation (1) can be rewritten as follows
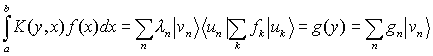 (6)
(6)
Using completeness (4) and orthogonality (5), the above equation is reduced to the following set of equations for the expansion coefficients
![]()
It can be easy resolved
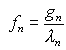
and the unknown function can be reconstructed
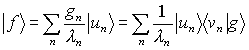 (7)
(7)
Pseudo-inverse operator
We can introduce the pseudo-inverse operator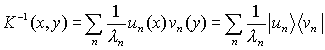 (8)
(8)
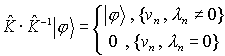
![]()
References
- V.S.Bashurova, K.P.Koutsenogii, A.Yu.Pusep, N.V.Shokhirev. Determination of atmospheric aerosol size distribution functions from screen diffusion battery data: Mathematical aspects. J.Aerosol Sci., v.22, p.373-388, 1991.
- A.Yu.Pusep, V.S.Bashurova, N.V.Shokhirev A.I.Burshtein. The development of the software for NMR-tomography of underground water. Tech. Report of the Institute of Chemical Kinetics and Combustion. Academy of Sciences of the USSR, Novosibirsk, 1991.
- N.V.Shokhirev, L.A.Rapatskii, A.M.Raitsimring. Electron-ion pair distribution function reconstructed from radiation-chemical and photochemical experiments. Chem.Phys., v.105, p.117-126, 1986.
- A.Yu.Pusep, N.V.Shokhirev. Determination of particle-size distribution functions in aerosols from measurements by diffusion batteries. Colloid J., v.48, p.108-113, 1986.
- N.V.Shokhirev, V.V.Konovalov, A.Yu.Pusep, and A.M.Raitsimring. Recovering the e-aq distribution in Photoemission. Theor.Exper.Chem., v.20, p.316-321, 1984.
- A.Yu.Pusep, N.V.Shokhirev. Application of a singular expansion for analyzing spectroscopic inverse problems. Opt.Spectrosc., v.57, p.482-486, 1984.