Introduction

Object definitions

A matrix is a  rectangular array of numbers () _{i, j} =  x _{i, j} , i = 1, .., N;  j = 1, .., M :

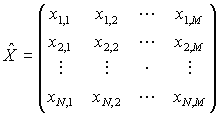
(1)

Here N is the number of rows and M is the number of columns ( N by M matrix).

The transpose of a matrix is another matrix, produced by turning rows into columns and vice versa. It is usually denoted by the superscript T. 

(X T ) i, j = (X) j, i

(2)

Obviously (X ^T ) is an M by N matrix.

A vector is a linear array of numbers y _{i, j} , i = 1, .., N:

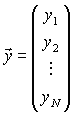
(3)

It can be considered as an N by 1 matrix. It is also called as a column vector.

Another particular case of a matrix is a row vector:

(4)

It can be considered as an 1 by M matrix and it is the transpose of a column vector.

Operations

For any object (matrix or vector) a multiplication by a scalar is defined as a multiplication of each element (component) by the scalar:

(c · X ) i, j =  c · x i, j

(5)

For the objects of the same dimension the addition and subtraction are defined as 

(A ± B) i, j = a i, j ± b i, j

(6)

The product C of two matrices A and B is defined as

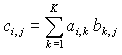
(7)

 Eq. (7) implies the following relationship between the dimensions of the matrices

Matrix	Dimensions
A	N by K
B	K by M
C	N by M

Matrix multiplication is associative:

(A · B) · C = A · (B · C) = A · B · C

(8)

However, matrix multiplication in general is not commutative:

A · B ≠ B · A

(9)

 In the case M = 1 and N =  1 Eq. (7) reduces to the dot product of inner product of two vectors. In this case C is an 1 by 1 matrix, i.e. a scalar:

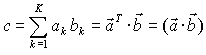
(10)

 

 In the case K = 1 Eq. (7) reduces to the direct or outer product of two vectors. In this case C id an N by M matrix:

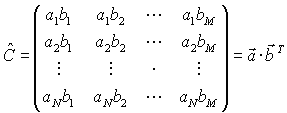
(11)

 Particular cases

 The matrix X (1) is square if N = M. 

A diagonal matrix is a square matrix A of the form

a i, j = a i  δ i, j

(12)

where δ _{i, j}  is the Kronecker delta

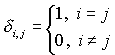
(13)

 

Useful formulae

  Transposition of a product

(A · B) T = B T · A T

(14)

  Inversion of a product

(15)

Woodbury matrix identity

(16)

 

References

1. Woodbury matrix identity http://en.wikipedia.org/wiki/Woodbury_matrix_identity
2. Matrix Inverse in Block Form by J.-S. Roger Jang, 2001-03-21 http://www.cs.nthu.edu.tw/~jang/book/addenda/matinv/matinv/