Problem statement

In science and technology systems (objects) are characterized by a finite set of parameters: x_i ,  i = 1, ... , N. Consequently, the measurements for these parameters can be arranged into a rectangular matrix:

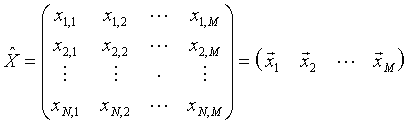
(1)

Here M is the number of experiments. Each experiment corresponds to the measurement of a system , sample, individual, etc. All such terms are used interchangeably.  

Examples

Systems	Parameters
Human individuals	Age, sex, education, income, weight, height, etc.
Chemical solutions	Spectral intensities at selected wavelength
Microchips in a control sample	Voltage and current at certain pins
Clinical test participants	Lab test results

 

Mean values

The sample (population) mean vector of parameters is defined as:

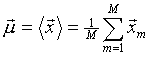
(2)

For each measurement the vector of deviations can be defined as:

(3)

In the case of clinical research, one of the components of μ is an average patient temperature in a hospital. Obviously, more interesting is a deviation from this average.

The vectors of deviations form the matrix D similar to the initial matrix X:

(4)

Covariance matrix

The sample covariance matrix is defined as averaged products of the deviation vector components:

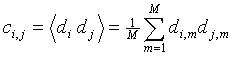
(5)

Here d_i,m is the i-th parameter of the m-th system.

Eq (5) can be rewritten in the following matrix form:

(6)

The superscript "T" denotes the matrix transposition.

Variances

The maximum likelihood covariance matrix C^ML differs by the factor M /(M-1) from the above definition:

.

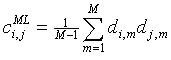(7)

The advantage of this definition is that the i-th diagonal element is the estimation for the variances of the  i-th parameter:

(8)

Correlation coefficient

Regardless of the covariance definition, the correlation coefficients are:

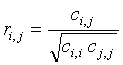
(9

or in a matrix form:

(10)

Here is a diagonal matrix with the following matrix elements:

(1)

The correlation coefficient is a measure of the quality of a linear least squares fit for the original data. A higher σ value means a better linear fit.

 

This approach is implemented in a program called "Correlations". This program is available in the Download section below. You can also use more general "Stat Analysis" program.

Remark: In "Correlations" the meaning of the columns and rows is opposite to that of the tutorial.

Download

1. Program "Correlations".
2. Program "Stat Analysis".

References

1. Correlation and dependence.