Numerical experiments, Tips, Tricks and Gotchas

Generating correlated random variables
Cholesky decomposition vs Square root decomposition
1. Problem statement
There are $n$ independent (uncorrelated) random variables $x_{1},x_{2},\ldots,x_{n}$ with zero means \begin{equation} \left\langle \vec{x}\right\rangle =\vec{0} \end{equation} and unit variances \begin{equation} \left\langle \vec{x}\cdot\vec{x}^{\mathrm{T}}\right\rangle =\hat{I}\label{eq:unitvar} \end{equation} Here the variables are arranged in n-dimensional vectors and the angle brackets denote averaging. The problem is to find a linear combination $\vec{y}$ of the variables $\vec{x}$ with a given covariance matrix $\hat{C}$: \begin{equation} \hat{C}=\left\langle \vec{y}\cdot\vec{y}^{\mathrm{T}}\right\rangle \label{eq:cov} \end{equation} In other words, it is necessary to find a transformation matrix $\hat{M}$ \begin{equation} \vec{y}=\hat{M}\cdot\vec{x}\label{eq:Mx} \end{equation} so that the equality (\ref{eq:cov}) takes place.2. Solution
Substituting (\ref{eq:Mx}) into (\ref{eq:cov}) and taking into account (\ref{eq:unitvar}) we get: \begin{equation} \hat{C}=\left\langle \hat{M}\cdot\vec{x}\cdot\vec{x}^{\mathrm{T}}\cdot\hat{M}^{\mathrm{T}}\right\rangle =\hat{M}\cdot\left\langle \vec{x}\cdot\vec{x}^{\mathrm{T}}\right\rangle \cdot\hat{M}^{\mathrm{T}}=\hat{M}\cdot\hat{M}^{\mathrm{T}}\label{eq:MMT} \end{equation} Any matrix $\hat{M}$ that satisfies (\ref{eq:MMT}) solves the problem.2.1. Cholesky decomposition
The form of Eq.(\ref{eq:MMT}) suggests that we can use the Cholesky decomposition. Indeed, a covariance matrix is supposed to be symmetric and positive-definite. It always can be decomposed into the product of a lower triangular matrix $\hat{L}$ and its transpose [1]: \begin{equation} \hat{C}=\hat{L}\cdot\hat{L}^{\mathrm{T}} \end{equation}2.1.1. Example
For the correlation matrix of two variables \begin{equation} \hat{C}=\left[\begin{array}{cc} 1 & \rho\\ \rho & 1 \end{array}\right]\label{eq:C2x2} \end{equation} The decomposition is \begin{equation} \hat{L}=\left[\begin{array}{cc} 1 & 0\\ \rho & \delta \end{array}\right]\label{eq:chol} \end{equation} Here $\delta=\sqrt{1-\rho^{2}}$.2.2. Square root decomposition
A symmetric and positive-definite matrix $\hat{C}$ can be presented as \begin{equation} \hat{C}=\hat{S}^{2} \end{equation} Here $\hat{S}$ is a square root of $\hat{C}$, which can be also chosen as symmetric $\hat{S}=\hat{S}^{\mathrm{T}}$and positive-definite [2].2.2.1. Example
For the matrix (\ref{eq:C2x2}) the square root is \begin{equation} \hat{S}=\left[\begin{array}{cc} c & s\\ s & c \end{array}\right]\label{eq:sqrt} \end{equation} where \begin{eqnarray} c & = & \sqrt{\frac{1+\delta}{2}}\\ s & = & \sqrt{\frac{1-\delta}{2}} \end{eqnarray}2.3. More solutions
If $\hat{M}$ is a solution of (\ref{eq:MMT}) then its product with an arbitrary orthogonal matrix [3] $\hat{U}$ \begin{equation} \hat{M^{\prime}}=\hat{M}\cdot\hat{U} \end{equation} is also a solution of (\ref{eq:MMT}). \begin{equation} \hat{M^{\prime}}\cdot\hat{M^{\prime}}^{\mathrm{T}}=\hat{M}\cdot\hat{U}\cdot\hat{U}^{\mathrm{T}}\cdot\hat{M}^{\mathrm{T}}=\hat{M}\cdot\hat{M}^{\mathrm{T}} \end{equation}3. Do we need many solutions?
In the important case of the multivariate normal (Gaussian) distribution we do not need this. The normal distribution is completely defined by its mean and covariance [4]. In general, however, different transformations result in different shape of the distribution functions.3.1. 2D example
Suppose variables $x_{1}$and $x_{2}$ are uniformly distributed in the intervals $[-\frac{1}{2},\frac{1}{2}]$. The vector $\vec{x}$ is uniformly distributed in the unit square: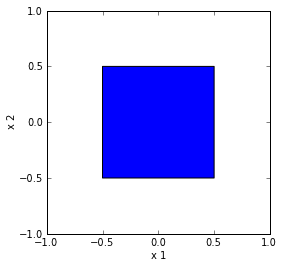
Fig. 1. 2D uniform distribution.
3.1.1. Cholesky decomposition
The transformation (\ref{eq:chol}) with $\rho=\frac{1}{2}$ results in the following distribution for $\vec{y}$ :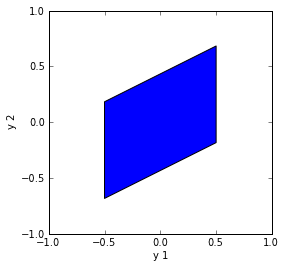
Fig. 2. Cholesky decomposition.
3.1.2. Square root decomposition
The transformation (\ref{eq:sqrt}) with the same $\rho=\frac{1}{2}$ gives more symmetric distribution for $\vec{y}$ :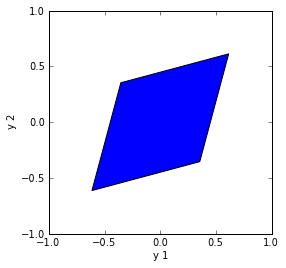
Fig. 3. Square root decomposition.
4. Implementation
4.1. Cholesky decomposition
Cholesky decomposition [1] is a standard routine in many linear algebra packages.4.2. Square root decomposition
There are several iterative algorithms [2]. I use diagonalization \begin{equation} \hat{C}=\hat{U}\cdot\hat{c}\cdot\hat{U}^{\mathrm{T}} \end{equation} \begin{equation} \hat{C}^{\frac{1}{2}}=\hat{U}\cdot\hat{c}^{\frac{1}{2}}\cdot\hat{U}^{\mathrm{T}} \end{equation} The marix $\hat{c}$ is diagonal $\left(\hat{c}\right)_{i,j}=c_{i,i}\delta_{i,j}$ and $\left(\hat{c}^{\frac{1}{2}}\right)_{i,j}=\delta_{i,j}\,\sqrt{c_{i,i}}$ .4.3. Steps
It is convenient to split the implementation into the following steps.
0. Random numbersNeedless to say that one should start with good (pseudo-) random numbers $\vec{x}$.
1. Transformation to correlationFirst transform $\vec{x}$ to get a correlation matrix \begin{equation} \hat{R}=\hat{M}\cdot\hat{M}^{\mathrm{T}} \end{equation} where \begin{equation} R_{i,j}=\begin{cases} 1 & i=j\\ \rho_{i,j} & i\neq j \end{cases} \end{equation} This is the most time-consuming step and can be performed once. Usually a correlation matrix is needed anyway.
2. Transform to covariance \begin{equation} \hat{C}=\hat{\sigma}\cdot\hat{R}\cdot\hat{\sigma} \end{equation} Here $\hat{\sigma}$ is a diagonal matrix of standard deviations: \[ \sigma_{i,j}=\sigma_{i}\delta_{i,j} \] The new transformation \begin{equation} \hat{M^{\prime}}=\hat{\hat{\sigma}\cdot M} \end{equation} gives \begin{equation} C_{i,j}=\begin{cases} \sigma_{i}^{2} & i=j\\ \rho_{i,j}\sigma_{i}\sigma_{j} & i\neq j \end{cases} \end{equation} Problem solved.
References
- Wikipedia. Cholesky decomposition.
- Wikipedia. Square root of a matrix.
- Wikipedia. Orthogonal matrix.
- Wikipedia. Multivariate normal distribution