The power of orthogonality
(based on a real story)
November 14, 2011
1. Introduction
Once I was approached with the request to rewrite in supposedly fast C++ a "slow" visual basic program. That program was a GUI for a spectrometer. Due to technical limitations, the measurements could be done only in relatively few points. However, all intermediate points were necessary for the purposes of display and further processing. Namely this part of the program was slow and unstable.
2. Problem statement
An instrument can measure a spectrum at M channels:
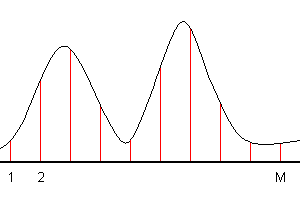
In other words, there are the values F1, F2, . . , FM at the points x1, x2, . . , xM. It is necessary to get a spectrum at any arbitrary value x within the interval of measurements ( x1≤ x ≤ xM ).
3. Naïve solution
According to the Weierstrass theorem [1], every continuous function can be uniformly approximated as closely as desired by a polynomial function. The "obvious" solution is to present the spectrum as a polynomial
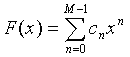
|
(1) |
The polynomial coefficients are the solution of the following system of linear equations:
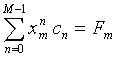
|
(2a) |
or in a matrix-vector form
| |
(2b) |
Here Amn = xmn is the Vandermonde matrix [2]. If all xi are different (which is the case) then the determinant of A ≠ 0 and Eq. (2) can always be solved:
| |
(3) |
The polynomial (1) with coefficients (3) exactly fits the measurements.
Remark 1. The solution of (2) is a time consuming problem (e.g. the computational complexity for the Gauss–Jordan elimination [3] is O(M 3) [4] ). This solution should be done for each new spectrum. However, the solution should not be performed for each x in (1). This actually solved "the slowness" of the VB program.
Remark 2. The polynomial (1) is a linear combination of the power functions (1, x, x2, . . ). If this basis set is not "natural" for the problem, then the interpolation between channels may be very poor.
Remark 3. The matrix Amn = xmn of the system of liner equations (2) is usually ill-conditioned [ 5]. The reason for this is that in a relatively narrow interval of positive values of x all powers look alike and are almost linear dependent. This makes the solution unstable and inaccurate.
Trick: use y = x - xav in (1) instead of x. Here xav is the middle of the spectrum. This trick partly solves the problem for relatively small M.
Remark 4. The solution of (2) is a time consuming problem ( complexity of M 3 ).
4. Optimized solution
1. Let us admit that there are strong physical reasons for a polynomial representation (1) for a spectrum.
2. Instead of using pure power basis function (1) we use the polynomials Pk(x)
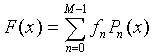 |
(4) |
orthogonal on the set of measurements:
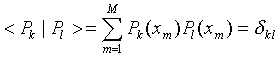 |
(5) |
3. The coefficients fn can be easy found in one step:
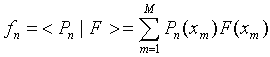 |
(6) |
The solution (6) is fast, stable and accurate because of the orthogonality condition (5). For the solution it is actually necessary to know only the matrix Pn(xm).
5. Orthogonal basis construction
Initially we have a liner independent set of the power functions: 1, x, x2, . . , xM-1 . We will construct an orthogonal polynomials recursively.
Suppose that we already constructed P0, P1, . ., Pn that are mutually orthogonal and normalized. The next polynomial is made of the new power xn+1 and all previous polynomials:
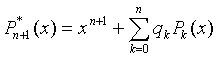 |
(7) |
The coefficients qk should be chosen to make (6) orthogonal to all previous polynomials:
| (8) |
or
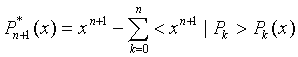 |
(9) |
The final stage is to normalize the new polynomial:
| (10) |
The initial normalized polynomial is
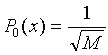 |
(11) |
Remark 1. Eq. (9) is the subtraction of all previous Pk-components from xn+1 (actually from all functions of the old basis).
Remark 2. The above relatively complex procedure have to be performed only once for a given set of points x1, x2, . . , xM.
Remark 3. This procedure can be applied to any set of linear independent basis functions.
6. Examples
1. Non-centered points
Let us consider four equidistant points: x1 = 1, x2 = 1.33333333333333, x3 = 1.66666666666667, x4 = 2. The initial functions are the powers of x: 1, x, x2, x3. Below is the matrix of their scalar products <xk|xn>. The power functions are normalized: <xn|xn> = 1.
| 1 | x | x2 | x3 | |
| 1 | 1 | 0.970494958830946 | 0.904912290402514 | 0.833821472585545 |
| x | 0.970494958830946 | 1 | 0.980330585324433 | 0.939926806394817 |
| x2 | 0.904912290402514 | 0.980330585324433 | 1 | 0.988499732201293 |
| x3 | 0.833821472585545 | 0.939926806394817 | 0.988499732201293 | 1 |
This matrix is related to xmn It is extremely ill-conditioned matrix. Its eigenvalues are:
{ ![]() } =
{0.00000022343673427,
0.00172815339820463,
0.187758070383405, 3.81051154185105}. The condition number is defined as cond
= Max(
} =
{0.00000022343673427,
0.00172815339820463,
0.187758070383405, 3.81051154185105}. The condition number is defined as cond
= Max(![]() )/Min(
)/Min(![]() ).
For the above matrix cond = 1.7 E 7. The larger the condition number is
the closer a matrix to a singular one. The condition number is a measure of
noise and round off errors amplification. A matrix is considered as
well-conditioned if cond << 102.
).
For the above matrix cond = 1.7 E 7. The larger the condition number is
the closer a matrix to a singular one. The condition number is a measure of
noise and round off errors amplification. A matrix is considered as
well-conditioned if cond << 102.
The coefficients of new orthogonal polynomials are:
| C0 | C1 | C2 | C3 | |
| P0 | 0.5 | 0 | 0 | 0 |
| P1 | -2.01246117974981 | 1.34164078649987 | 0 | 0 |
| P2 | 9.5 | -13.5 | 4.5 | 0 |
| P3 | -61.0446557857441 | 131.257190279237 | -90.5607530887411 | 20.124611797498 |
Below is the matrix <Pn|Pk> :
| P0 | P1 | P2 | P3 | |
| P0 | 1.00000000000000 | 4.44 E-16 | -7.55 E-15 | 5.51 E-14 |
| P1 | 4.44 E-16 | 1.00000000000000 | 6.11 E-16 | -1.66 E-14 |
| P2 | -7.55 E-15 | 6.11 E-16 | 0.999999999999999 | -4.42 E-14 |
| P3 | 5.51 E-14 | -1.66 E-14 | -4.42 E-14 | 0.999999999999935 |
This matrix is close to the identity matrix despite the large cond value.
2. Centered points (using the trick)
Now the points are: x1 = -0.5, x2 = -0.16666666666667, x3 = 0.16666666666667, x4 = 0.5. In this case the matrix <xk|xn> is:
| 1 | x | x2 | x3 | |
| 1 | 1 | -1.12 E-16 | 0.78086880944303 | -1.18 E-16 |
| x | -1.12 E-16 | 1 | -1.57 E-16 | 0.959737407008271 |
| x2 | 0.78086880944303 | -1.57 E-16 | 1 | -2.76 E-16 |
| x3 | -1.18 E-16 | 0.959737407008271 | -2.76 E-16 | 1 |
The even and odd powers are already orthogonal and the eigenvalues are: {0.0402625929917295, 0.21913119055697, 1.78086880944303, 1.95973740700827}. This gives cond = 48.7.
The constructed orthogonal polynomials include only the power of the same
parity:
| C0 | C1 | C2 | C3 | |
| P0 | 0.50000000000000 | 0 | 0 | 0 |
| P1 | 5.58 E-17 | 1.34164078649987 | 0 | 0 |
| P2 | -0.6250000000000 | 2.51 E-16 | 4.5000000000000 | 0 |
| P3 | -1.67 E-16 | -4.58393935387457 | 1.33 E-15 | 20.1246117974981 |
The matrix <Pn|Pk> now is closer to the identity matrix:
| P0 | P1 | P2 | P3 | |
| P0 | 1 | 5.55 E-17 | -5.55 E-17 | 1.11 E-16 |
| P1 | 5.55 E-17 | 1 | 0 | 6.38 E-16 |
| P2 | -5.55 E-17 | 0 | 1 | 3.88 E-16 |
| P3 | 1.11 E-16 | 6.38 E-16 | 3.88 E-16 | 1 |
The polynomial coefficients are calculated with higher accuracy.